最近在学习复习《数据结构与算法分析》,对一些典型的排序算法自己用Java实现,在这个练习的过程中加深对算法的了解。
选择排序(Selection sort)
是一种简单直观的排序算法,我觉得基本上是你面对排序问题时最先想到的方法。在未排序序列中找到最小或是最大的元素,存放到排序序列的起始位置;然后再从剩余的未排序的元素中继续寻找最小或是最大的元素。这样子持续进行下去,直到所有的元素排好顺序。往往最先想到的方法能解决问题,但是不能更好的解决问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| package com.boxing.algorithm;
public class SelectionSort implements SortAlgorithm {
@Override
public int[] doSort(int[] array) {
int min;
for (int index = 0; index < array.length - 1; index++) {
min = index;
for (int temp = index + 1; temp < array.length; temp++) {
if (array[temp] < array[min]) min = temp;
}
swapNumbers(array, min, index);
}
return array;
}
private void swapNumbers(int[] array, int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class SelectionSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new SelectionSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。
冒泡排序(Bubble sort)
冒泡排序,也叫sinking sort,是一种简单的排序算法。它重复地遍历要排序的数组,比较每一对相邻的元素,如果它们次序错误,就把它们进行交换。它的名字来自这种相对小的元素“上浮”到数组的顶部的方式。因为它对元素只用到了比较的操作方式,所以是一种比较排序。
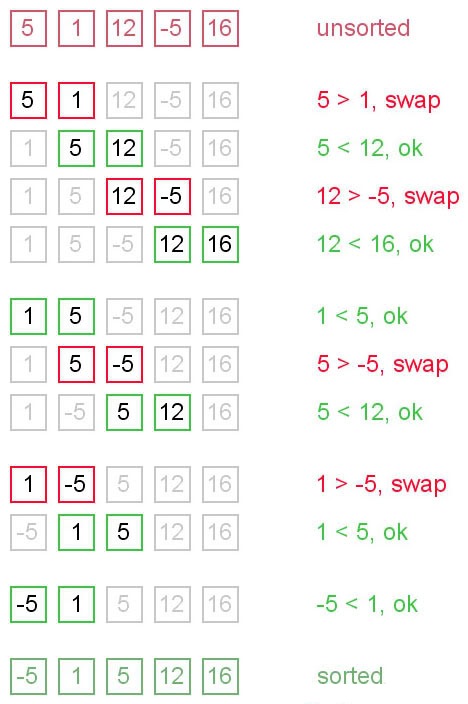
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| package com.boxing.algorithm;
public class BubbleSort implements SortAlgorithm {
@Override
public int[] doSort(int[] array) {
for (int index = 0; index<array.length-1;index++) {
for (int i = 0; i < array.length - 1-index; i++) {
if (isLargerThanAfter(array, i)) {
swapNumbers(array, i);
}
}
}
return array;
}
private boolean isLargerThanAfter(int[] array, int i) {
return array[i] > array[i + 1];
}
private void swapNumbers(int[] array, int i) {
int temp = array[i];
array[i] = array[i + 1];
array[i + 1] = temp;
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class BubbleSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new BubbleSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。
插入排序(Insertion sort)
插入排序是最简单的排序算法。它每次排好最终结果数组的一个元素。
它的一般原理是第p次时,将位置p上的元素向左移动,直到它在前p+1个元素中的正确位置被找到。
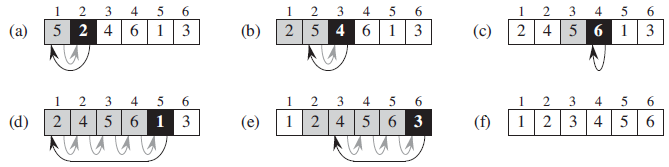
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| package com.boxing.algorithm;
public class InsertionSort implements SortAlgorithm {
@Override
public int[] doSort(int[] array) {
int temp;
for (int index = 1; index < array.length; index++) {
temp = array[index];
int i = index;
while (i > 0 && array[i - 1] > temp) {
array[i] = array[i - 1];
i--;
}
array[i] = temp;
}
return array;
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class InsertionSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new InsertionSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。
希尔排序(Shell sort)
希尔排序是对插入排序的一种改进。
插入排序有下面两个性质:
希尔排序通过比较相距一定间隔的元素来工作,每次排序比较所用的距离随着算法的进行而减小,直到只比较相邻元素的最后一次排序为止。这样一个所用距离的序列叫做增量序列(increment sequence)。
也就是对于这样的一组数:{ 13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39, 10 },如果我们以距离5开始进行排序,它们看起来是这样的:
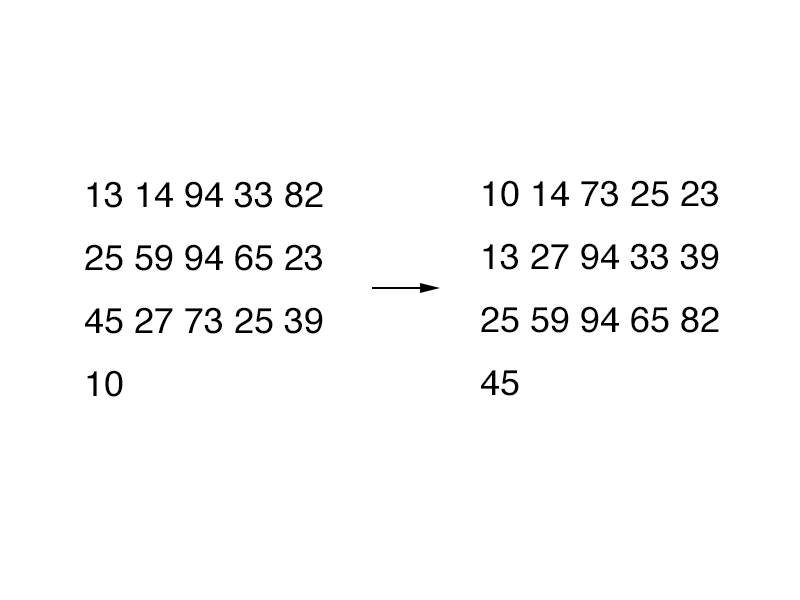
也就是说对每列进行了排序,得到了数组{ 10, 14, 73, 25, 23, 13, 27, 94, 33, 39, 25, 59, 94, 65, 82, 45 },可以发现,此时10已经到了正确的位置上。再以距离3对数组进行排序:
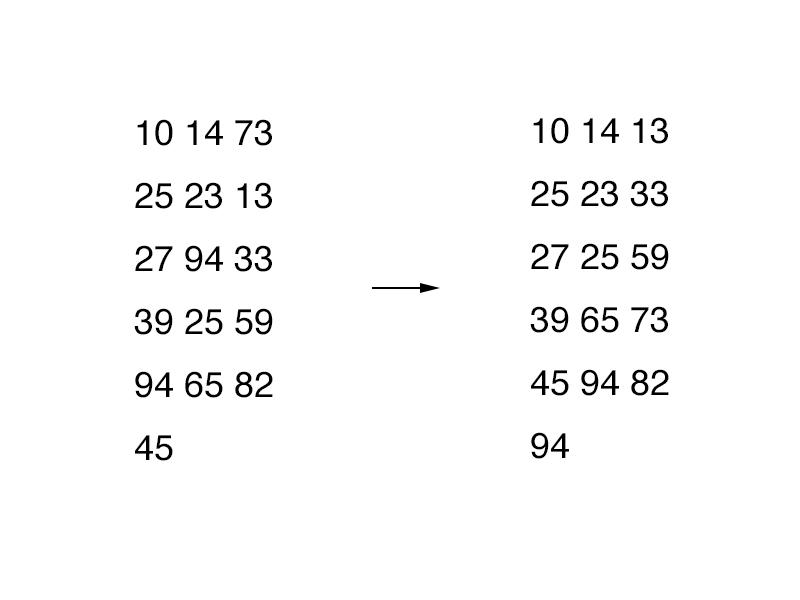
最后以距离1进行排序,也就是简单的插入排序了。
目前已知最好的增量序列是Sedgewick提出的,{ 1, 5, 19, 41, 109, … },该序列中的项要么是(9×4i-9×2i+1),要么是(4i-3×2i+1)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| package com.boxing.algorithm;
public class ShellSort implements SortAlgorithm {
@Override
public int[] doSort(int[] array) {
int gap = 1;
while (gap < array.length / 3) {
gap = gap * 3 + 1;
}
for (; gap >= 1; gap /= 3) {
for (int k = 0; k < gap; k++) {
for (int i = gap + k; i < array.length; i += gap) {
for (int j = i; j >= gap && array[j] < array[j - gap]; j -= gap) {
swapNumbers(array, j, j - gap);
}
}
}
}
return array;
}
private void swapNumbers(int[] array, int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class ShellSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new ShellSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。
归并排序(Merge sort)
这个算法中基本的操作是把两个已排序的序列合并成一个序列。
归并的操作过程为:
创建一个空序列,使其大小为两个已排序的序列之和;
设定两个计数器,最初的位置分别为两个已经排序序列的起始位置;
比较两个计数器处元素的大小,选择相对小的元素放入空序列中,对应的计数器向前推进一步;
重复步骤3直到某一计数器到达序列尾;
将另一序列中剩下的所有元素复制到空序列中。
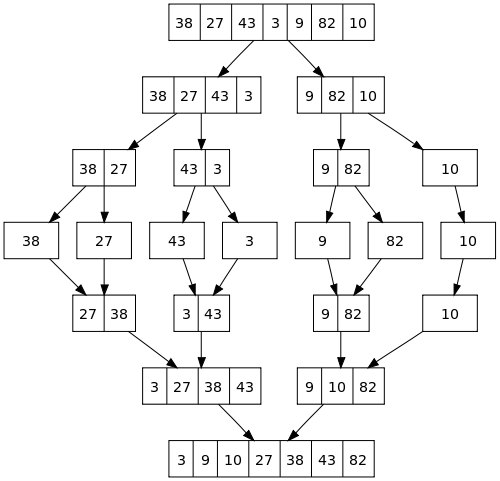
该算法是经典的分治(divide-and-conquer)策略,它将问题(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段解得的各答案修补在一起。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| package com.boxing.algorithm;
public class MergeSort implements SortAlgorithm {
private int[] array;
private int[] helper;
@Override
public int[] doSort(int[] array) {
this.array = array;
this.helper = new int[array.length];
mergeSort(0, array.length - 1);
return this.array;
}
private void mergeSort(int low, int high) {
if (low < high) {
int middle = low + (high - low) / 2;
mergeSort(low, middle);
mergeSort(middle + 1, high);
merge(low, middle, high);
}
}
private void merge(int low, int middle, int high) {
System.arraycopy(array, low, helper, low, high + 1 - low);
int i = low;
int j = middle + 1;
int k = low;
while (i <= middle && j <= high) {
if (helper[i] <= helper[j]) {
array[k] = helper[i];
i++;
} else {
array[k] = helper[j];
j++;
}
k++;
}
while (i <= middle) {
array[k] = helper[i];
k++;
i++;
}
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class MergeSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new MergeSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。
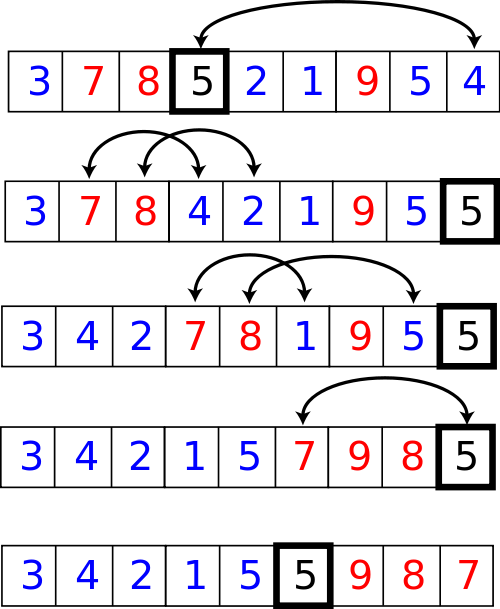
快速排序(Quick sort)
快速排序是实践中一种快速的排序算法。它是一种分治的递归算法。它首先把一个大的数组分成两个小的子数组:较小的数的数组和较大的数的数组。再对这子数组做递归处理。
实现快速排序的步骤:
从数组中任意选择一个元素,称为枢纽元(pivot)。虽然无论选择哪个元素作为pivot都可以完成排序,但是有些选择显然优于其他选择。将第一个元素作为pivot是一种错误的做法。安全的做法是随机选取pivot。最好的做法是选择数组的中值:一般的做法是使用左端、右端和中心位置上的三个元素的中值作为pivot。
对数组进行重新排序,所有比pivot小的数在pivot前面,所有比pivot大的数在pivot后面(相等的可以在任何一边)。经过这样的分区后,pivot就在它最终的位置上了。这个步骤叫做分区操作。
把上述的步骤对含有较小数的子数组和含有较大数的子数组进行递归操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| package com.boxing.algorithm;
public class QuickSort implements SortAlgorithm {
int[] array;
@Override
public int[] doSort(int[] array) {
this.array = array;
doQuickSort(this.array, 0, this.array.length - 1);
return this.array;
}
private void doQuickSort(int[] array, int left, int right) {
int i = left, j = right;
int pivot = median(array, left, right);
while (i <= j) {
while (array[i] < pivot) {
i++;
}
while (array[j] > pivot) {
j--;
}
if (i <= j) {
swapNumbers(array, i, j);
i++;
j--;
}
}
if (left < j)
doQuickSort(array, left, j);
if (i < right)
doQuickSort(array, i, right);
}
private int median(int[] array, int left, int right) {
int center = (left + right) / 2;
if (array[left] > array[center])
swapNumbers(array, left, center);
if (array[left] > array[right])
swapNumbers(array, left, right);
if (array[center] > array[right])
swapNumbers(array, center, right);
swapNumbers(array, center, right - 1);
return array[right - 1];
}
private void swapNumbers(int[] array, int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
}
|
1
2
3
4
5
6
7
8
9
10
| public class QuickSortTest {
@Test
public void shouldInputAnArray_return_sortedArray() {
SortAlgorithm sortAlgorithm = new QuickSort();
int[] inputArray = {10, 34, 2, 56, 7, 67, 88, 42};
int[] outputArray = sortAlgorithm.doSort(inputArray);
assertThat(outputArray, is(new int[]{2, 7, 10, 34, 42, 56, 67, 88}));
}
}
|
测试通过。上面的快速排序算法使用左端、右端和中心位置上的三个元素的中值作为pivot。这是比较好的实践。
算法代码repo
“戳我戳我戳我~(≧▽≦)/~”
参考文献
数据结构与算法分析:Java语言描述
排序算法
Sorting Algorithm Animations





